返回 [Spark MLlib入门教程](http://mocom.xmu.edu.cn/article/show/5858ab782b2730e00d70fa08/0/1) --- ## 方法简介 ​ 逻辑斯蒂回归（logistic regression）是统计学习中的经典分类方法，属于对数线性模型。logistic回归的因变量可以是二分类的，也可以是多分类的。 ## 基本原理 ### logistic分布 ​ 设X是连续随机变量，X服从logistic分布是指X具有下列分布函数和密度函数： ​ $$F(x)=P(x \le x)=\frac 1 {1+e^{-(x-\mu)/\gamma}}$$ ​ $$f(x)=F^{'}(x)=\frac {e^{-(x-\mu)/\gamma}} {\gamma(1+e^{-(x-\mu)/\gamma})^2}$$ ​ 其中，$\mu$为位置参数，$\gamma$为形状参数。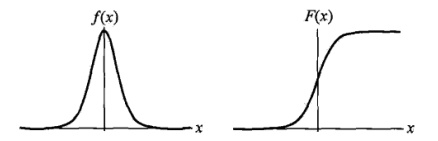 ​ $f(x)$与$F(x)$图像如下，其中分布函数是以$(\mu, \frac 1 2)$为中心对阵，$\gamma$越小曲线变化越快。 #####  ### 二项logistic回归模型： ​ 二项logistic回归模型如下： ​ $$P(Y=1|x)=\frac {exp(w \cdot x + b)} {1 + exp(w \cdot x + b)}$$ ​ $$P(Y=0|x)=\frac {1} {1 + exp(w \cdot x + b)}$$ ​ 其中，$x \in R^n$是输入，$Y \in {0,1}$是输出，w称为权值向量，b称为偏置，$w \cdot x$为w和x的内积。 ### 参数估计 ​ 假设： ​ $$P(Y=1|x)=\pi (x), \quad P(Y=0|x)=1-\pi (x)$$ ​ 则采用“极大似然法”来估计w和b。似然函数为: ​ $$\prod_{i=1}^N [\pi (x_i)]^{y_i} [1 - \pi(x_i)]^{1-y_i}$$ ​ 为方便求解，对其“对数似然”进行估计： ​ $$L(w) = \sum_{i=1}^N [y_i \log{\pi(x_i)} + (1-y_i) \log{(1 - \pi(x_i)})]$$ ​ 从而对$L(w)$求极大值，得到$w$的估计值。求极值的方法可以是梯度下降法，梯度上升法等。 ### 示例代码 ​ 我们以iris数据集（[https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data](https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data)）为例进行分析。iris以鸢尾花的特征作为数据来源，数据集包含150个数据集，分为3类，每类50个数据，每个数据包含4个属性，是在数据挖掘、数据分类中非常常用的测试集、训练集。 #### 1. 导入需要的包： ```scala import org.apache.spark.SparkConf import org.apache.spark.SparkContext import org.apache.spark.mllib.classification.{LogisticRegressionWithLBFGS, LogisticRegressionModel} import org.apache.spark.mllib.evaluation.MulticlassMetrics import org.apache.spark.mllib.regression.LabeledPoint import org.apache.spark.mllib.linalg.{Vectors,Vector} ``` #### 2. 读取数据： ​ 首先，读取文本文件；然后，通过map将每行的数据用“,”隔开，在我们的数据集中，每行被分成了5部分，前4部分是鸢尾花的4个特征，最后一部分是鸢尾花的分类。把这里我们用LabeledPoint来存储标签列和特征列。 LabeledPoint在监督学习中常用来存储标签和特征，其中要求标签的类型是double，特征的类型是Vector。这里，先把莺尾花的分类进行变换，"Iris-setosa"对应分类0，"Iris-versicolor"对应分类1，其余对应分类2；然后获取莺尾花的4个特征，存储在Vector中。 ```scala scala> val data = sc.textFile("G:/spark/iris.data") data: org.apache.spark.rdd.RDD[String] = G:/spark/iris.data MapPartitionsRDD[1] at textFile at :28 scala> val parsedData = data.map { line => | val parts = line.split(',') | LabeledPoint(if(parts(4)=="Iris-setosa") 0.toDouble else if (parts(4) =="Iris-versicolor") 1.toDouble else | 2.toDouble, Vectors.dense(parts(0).toDouble,parts(1).toDouble,parts (2).toDouble,parts(3).toDouble)) | } parsedData: org.apache.spark.rdd.RDD[org.apache.spark.mllib.regression.LabeledPo int] = MapPartitionsRDD[2] at map at :30 ``` ​ 然后，把数据打印看一下： ```scala scala> parsedData.foreach { x => println(x) } (1.0,[6.0,2.9,4.5,1.5]) (0.0,[5.1,3.5,1.4,0.2]) (1.0,[5.7,2.6,3.5,1.0]) (0.0,[4.9,3.0,1.4,0.2]) (1.0,[5.5,2.4,3.8,1.1]) (0.0,[4.7,3.2,1.3,0.2]) (1.0,[5.5,2.4,3.7,1.0]) (0.0,[4.6,3.1,1.5,0.2]) ... ... ``` #### 3. 构建模型 ​ 接下来，首先进行数据集的划分，这里划分60%的训练集和40%的测试集： ```scala scala> val splits = parsedData.randomSplit(Array(0.6, 0.4), seed = 11L) splits: Array[org.apache.spark.rdd.RDD[org.apache.spark.mllib.regression.Labeled Point]] = Array(MapPartitionsRDD[3] at randomSplit at :32, MapPartition sRDD[4] at randomSplit at :32) scala> val training = splits(0).cache() training: org.apache.spark.rdd.RDD[org.apache.spark.mllib.regression.LabeledPoin t] = MapPartitionsRDD[3] at randomSplit at :32 scala> val test = splits(1) test: org.apache.spark.rdd.RDD[org.apache.spark.mllib.regression.LabeledPoint] = MapPartitionsRDD[4] at randomSplit at :32 ``` ​ 然后，构建逻辑斯蒂模型，用set的方法设置参数，比如说分类的数目，这里可以实现多分类逻辑斯蒂模型： ```scala scala> val model = new LogisticRegressionWithLBFGS(). | setNumClasses(3). | run(training) model: org.apache.spark.mllib.classification.LogisticRegressionModel = org.apach e.spark.mllib.classification.LogisticRegressionModel: intercept = 0.0, numFeatur es = 8, numClasses = 3, threshold = 0.5 ``` ​ 接下来，调用多分类逻辑斯蒂模型用的predict方法对测试数据进行预测，并把结果保存在MulticlassMetrics中。这里的模型全名为LogisticRegressionWithLBFGS，加上了LBFGS，表示**Limited-memory BFGS**。其中，BFGS是求解非线性优化问题（L(w)​求极大值）的方法，是一种秩-2更新，以其发明者Broyden, Fletcher, Goldfarb和Shanno的姓氏首字母命名。 ```scala scala> val predictionAndLabels = test.map { case LabeledPoint(label, features) => | val prediction = model.predict(features) | (prediction, label) | } predictionAndLabels: org.apache.spark.rdd.RDD[(Double, Double)] = MapPartitionsR DD[56] at map at :40 ``` 这里，采用了test部分的数据每一行都分为标签label和特征features，然后利用map方法，对每一行的数据进行model.predict(features)操作，获得预测值。并把预测值和真正的标签放到predictionAndLabels中。我们可以打印出具体的结果数据来看一下： ```scala (0.0,0.0) (1.0,1.0) (0.0,0.0) (2.0,1.0) (0.0,0.0) (2.0,1.0) (0.0,0.0) (1.0,1.0) (0.0,0.0) ... ... ``` 可以看出，大部分的预测是对的。但第4行的预测与实际标签不同。 #### 4. 模型评估 ​ 最后，我们把模型预测的准确性打印出来： ```scala scala> val metrics = new MulticlassMetrics(predictionAndLabels) metrics: org.apache.spark.mllib.evaluation.MulticlassMetrics = org.apache.spark. mllib.evaluation.MulticlassMetrics@2bd9ef8c scala> val precision = metrics.precision precision: Double = 0.9180327868852459 scala> println("Precision = " + precision) Precision = 0.9180327868852459 ```